Déterminer l’ensemble de définition d’une fonction en Seconde
Cet article est la suite de Qu’est-ce qu’une fonction ?
Qu’est-ce-que l’ensemble de définition ?
Pour comprendre ce qu’est l’ensemble de définition (ou domaine de définition), il faut déjà avoir bien compris ce qu’est une fonction. Dans le précédent article, nous avons expliqué qu’une fonction est un procédé qui associe un nombre x à un autre nombre noté f(x) :
Et l’ensemble de définition dans tout ça ? C’est l’ensemble des nombres de départ : c’est l’ensemble des nombres x tels que leur image f(x) existe. On peut le noter Df.
Cet ensemble peut être simplement donné par l’énoncé de l’exercice. La phrase qui l’annonce est « la fonction f est définie sur …». Par exemple la fonction f est définie sur [0;+∞[ : ainsi les nombres x appartenant à l’intervalle [0;+∞[ pourront avoir une image par f. Les autres nombres ne pourront pas en avoir.
Mais parfois, l’énoncé demande à l’élève de déterminer lui-même l’ensemble de définition, soit à partir de l’expression de f(x), soit à partir de la représentation graphique de f. Voyons ces 2 méthodes distinctes.
Déterminer l’ensemble de définition à partir de l’expression de f(x)
Si on donne l’expression d’une fonction f, par exemple f(x)=x²+3x, l’ensemble de définition a priori sera l’ensemble de tous les réels de -∞ jusqu’à +∞. On pourra alors noter Df=
.
Pourquoi n’en serait-il pas toujours ainsi ? Tout simplement parce que certaines opérations ne sont pas autorisées. (On dit qu’elles ne sont pas définies). Pour vous en rendre compte, vous pouvez essayer de taper certaines opérations, 1:0 ou √(-3) : la calculatrice renverra un message d’erreur.
En seconde, il faut connaître 2 opérations interdites :
- diviser par zéro
- racine carrée d’un nombre négatif.
1er exemple :
Quel est l’ensemble de définition de la fonction f pour
f(x) existe si et seulement si :
2x-4≠0
2x≠4
x≠2
Tous les nombres réels sauf 2 pourront donc avoir une image. On note :
Df= -{2} ou Df= \{2}
ou encore Df=]-∞;2[∪]2;+∞[
2ème exemple :
Quel est l’ensemble de définition de la fonction g pour
g(x) existe si et seulement si :
8-2x≥0
-2x≥-8
x≤4
Tous les nombres inférieurs à 4 pourront avoir une image. On note :
Dg=]-∞;4]
Ci-dessous une vidéo avec deux autres exemples pour trouver l’ensemble de définition avec deux autres expressions algébriques :
Déterminer l’ensemble de définition à partir de la courbe représentative de f
Je rappelle ce que j’avais expliqué dans le précédent article : la courbe représentative de f est l’ensemble des points donc les coordonnées sont ( x ; f(x) ).
Si l’on veut trouver l’ensemble de définition, autrement dit l’ensemble des x, il suffit de lire graphiquement l’ensemble des abscisses des points de la courbe représentant f.
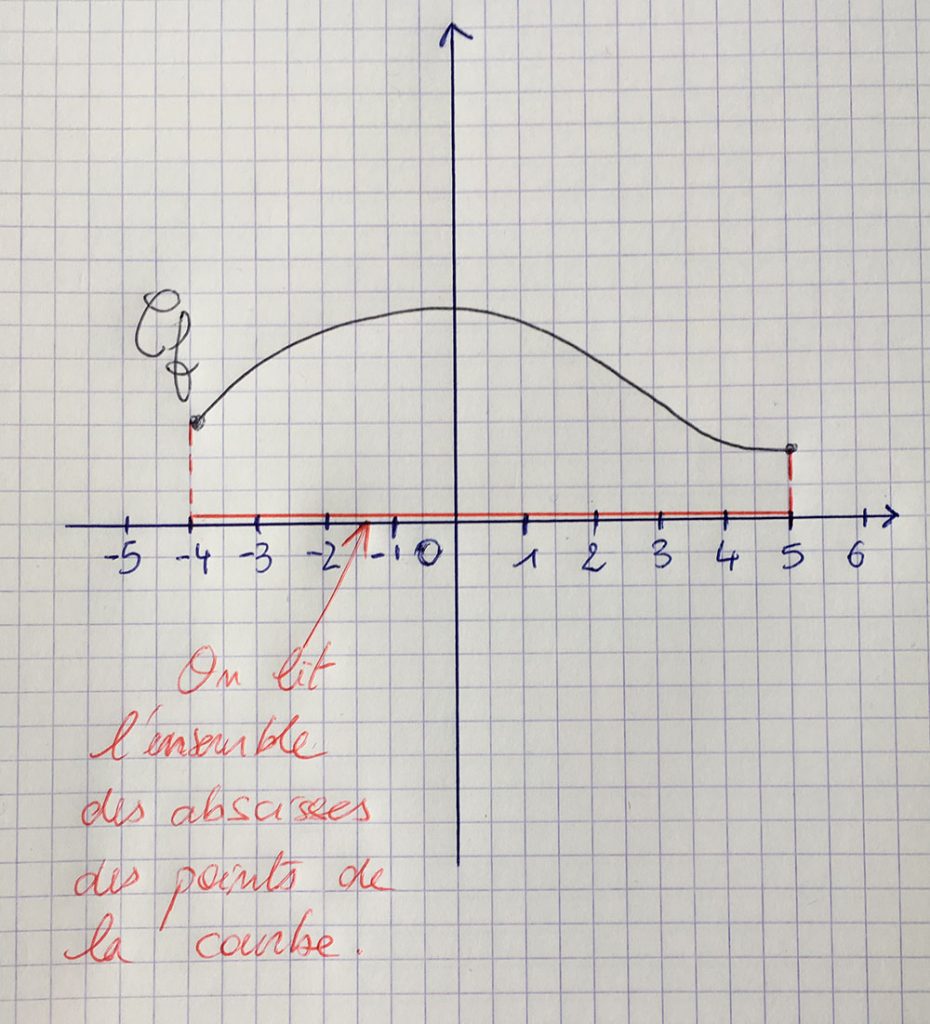
Voici un exemple illustré :
On lit les abscisses des points de la courbe représentative de f. Ici nous avons :
Df=[-4;5]
A vos commentaires !
Aide moi svp a éclaircir ce chapitre !!!
Volontiers
L’ensemble de définition de -(x-1)^2+4 est…?
Il n’y a pas de division ni de racine carrée. L’ensemble de définition de cette expression est donc l’ensemble des réels noté R. Ou l’intervalle ]-∞;+∞[ si tu préfères.
Salut, svp comment déterminer l’ensemble de définition de la fonction rationnelle où tout le dénominateur est au carré ?
Comme x+2 en haut au numérateur et (x+3) le tout au carré au carré au dénominateur.
Merci pour votre compréhension et j’aimerais que vous posiez les calculs.
Bonjour Kouassi Ivann,
Veux-tu dire cette fonction
?
j’ai besoin d’aide svp sur ce chapitre merci !
Volontiers si je puis être utile…
Oooh mais ça devient beaucoup plus clair maintenant ! C’en est même trop simple !
Merci beaucoup, vous m’avez sauvé moi et mes DM la veille ! 😀
Bonsoir et du coup si on lit les images de -4 : 0 et 2 par f quel est le résultat ?
Bonjour Mathieu,
Je suppose que tu me parles du graphique. Le soucis est que je n’ai pas mis d’échelle sur l’axe des ordonnées… En supposant qu’il s’agisse d’un repère orthonormé, l’image de -4 est 1,5 ; celle de 0 environ 3,2 et celle de 4 est 1.
J’ai besoin de votre aide svp
Un cours en ligne peut-être ?
Je veux plus d’éclaircissement sur la notion d’application.
Il s’agit de :
– application affine
– application linéaire
– application surjective
– application bijective
– application injective
Merci d’avance
Signé
Élisée ATONDE
Élève en classe de 2nde D
Pour toutes ces notions qui dépassent le cadre de notre article, il serait préférable d’envisager un stage pendant les vacances 😉
Bonsoir, pour trouver l’ensemble de définition d’une fonction à l’aide d’un graphique mais qui est du genre par partie (ce graphique). Comment faire ? merci.
Bonjour, tu fais une réunion d’intervalles, avec le symbole U.
Par exemple [-3;-1]U[1;2]
Salut…svp quelle est l’ensemble de définition de [(X²)-(X²)]/[X-X], existe t-elle?
Bonjour,
Curieuse question, ta fonction c’est 0/0 donc n’existe pas car on ne peut pas diviser par zéro.
Bonjour^^ dans une fonction, peut on mettre plusieurs U ? Par exemple :
[-7 ; -6] U [ -3 ; -2,5 ] U [ 2 ; 3,5 ] U [ 7,5 ; 8 ] ? Merci ^^
Bonjour, oui tu peux, rien ne l’empêche.
Bonjour j’aimerai bien que vous me confirmiez ma réponse svp
Il faut trouver l’ensemble de la définition.
f(x)=1/√x
J’ai mis que d(f)=R
Est ce juste, merci d’avance
Bonjour, non il faut que tu exclues 0. On ne peut pas diviser par zéro.
Donc ca va être :
]0;+infini[
Oui exactement.
Bonsoir , en ce qui concerne une équation de troisième degré , le domaine de définition est l’ensemble R ?
Bonjour, oui si la fonction est un polynôme, si l’ensemble de définition n’est pas précisé, alors ce sera R.
Thierry j’ai vraiment besoin d’aide pour le bac 2020 en maths, le 14 septembre je ferai le bac, pourriez-vous m’aidez svp ?
Juliette, vous pouvez m’appeler au 06 80 21 07 60. A bientôt !
Bonsoir, en fait je voudrais avoir toute les formules concernant les domaines de définition dans tous les cas…
Bonsoir, merci de ta question, c’est amusant d’y répondre même si je ne pourrai pas faire tous les domaines de définition de tous les cas. Voici les principaux auxquels je pense (il serait intéressant d’en rajouter) :
Les fonctions exponentielles sont définies sur ℝ, ainsi que les fonctions polynômes.
Les fonctions rationnelles sont définies pour les valeurs de x telles que le dénominateur ne s’annule pas.
La fonction racine carrée est définie sur [0;+∞[.
Les fonctions logarithmes sont définies sur ]0;+∞[.
Les fonctions cosinus et sinus sont définies sur ℝ, la fonction tangente sur ℝ privé des valeurs de π/2 modulo π.
Les fonctions arcos et arcsin sont définies sur [-1;1], la fonction arctan sur ℝ.
Voila c’est tout ce à quoi je pense pour l’instant…
Bonjour, j’aimerais une aide à mon exercice s’il vous plait…
énoncé : sois f la fonction définie par f(x) = -2x² + 1
1. Quel est son ensemble de définition D ?
2. Quelles sont les images de -2 ? de 5 ? de 0 ? et de 2√2 ?
3. Quels sont les antécédents éventuels de -3 ? de 0 ? et de 5 ?
Merci, une élève de 2nde.
Bonjour Mélissa,
1. Comme l’expression de f(x) ne contient ni division, ni racine carrée, l’ensemble de définition sera l’ensemble des réels R.
2. Dans l’expression de f(x) il suffit de remplacer x par les valeurs indiquées et de calculer les images.
3. Pour trouver les antécédents, il faut résoudre des équations…
excuse moi comment fait on pour déterminer l’ensamble de définition de ses fractions ? merci bien
f(x)=−5×2+3x−2
g(x)=x3+x2+x+1
Bonjour, manifestement ces expressions ne sont pas des fractions. Donc leur ensemble de définition est l’ensemble des réels R.
Bonjour. S’il vous plaît comment determiner l’ensemble de définition de cette fonction
|3x-7|
Bonjour, comme il n’y a ni division ni racine carrée, a priori l’ensemble de définition sera l’ensemble des réels R.
Merci Thierry tu es le meilleur
J’en doute mais merci !
Bonsoir, comment avez-vous trouvé le 4 en calculant l’ensemble de définition de f ?
Bonsoir,
-8 divisé par -2 cela fait 4.
Bonjour,
J’aimerais avoir une aide pour mon exercice s’il vous plaît …
On considère la fonction f définie par f(x)=(x² – 2)/ (x-1)
Soit (C) la courbe représentative de f dans la plan rapporté à un repère orthonormé (O;i;j)
1. Donner l’ensemble de définition D de f
2. Etudier les variations de f. On résumera les variations dans un tableau de variation.
3. Démontrer que pour tout xED, f(x) = x+1 – 1/(x-1)
4. Soit (d) la droite d’équation y=x+1
Etudier le signe de f(x)-(x+1) et en donner une interprétation graphique
5. Dans un repère, construire soigneusement (d), la droite d’équation x=1 puis (C)
Merci d’avance. Un élève de 1ERE
Bonjour Liam, je te réponds sur l’ensemble de définition qui est l’ensemble des réels privé de 1 : R\{1}
Bon courage !
Merci beaucoup pour votre réponse
Mes profondes salutations… Et merci à vous pour le travail que vous faites. Ma question est la suivante :
Je sais que ln(x) existe sur ]0; + infini [. Mais quel est le domaine de définition de ln(-x).
Bonjour, il faut que -x>0, soit x<0.
Donc le domaine de définition de ln(-x) est ]-∞;0[