En complément du cours sur le cercle trigonométrique – à lire avant cet article – nous expliquons aujourd’hui comment trouver la mesure principale d’un angle.
Avec ce présent cours et le précédent, vous aurez les bonnes bases pour comprendre la trigonométrie du lycée. Pour compléter vos connaissances, il sera certainement utile d’effectuer un stage pendant les vacances !
Rappels et compléments sur le cercle trigonométrique
Rappelons que le cercle trigonométrique est un cercle orienté, de rayon 1, dont le centre est l’origine d’un repère orthonormé.
A partir de l’axe des abscisses de ce repère nous mesurons des angles orientés. Par exemple sur le cercle trigonométrique ci-dessous est dessiné en rouge un angle dont la valeur est x :
Modulo 2π
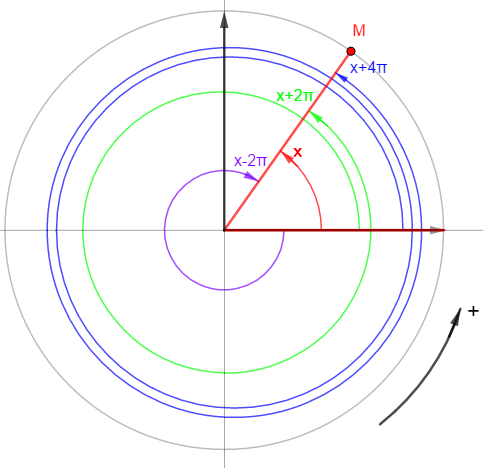
La figure ci-dessous montre comment un angle x auquel on ajoute 2π ou 4π ou -2π permet de repérer toujours le même point M sur le cercle trigonométrique :
Prenons par exemple l’angle π/3 qui repère le point M sur le cercle trigonométrique :
Ce même point M sera donc repéré sur le cercle par plusieurs mesures d’angles :
Toutes ces mesures d’angles repèrent sur le cercle le même point M. Elles valent toutes : . (
est l’ensemble des nombres entiers relatifs).
, c’est un peu long à écrire. On préfère donc l’écriture :
x[2π] qui se lit x modulo 2π.
La seule mesure qui appartient à l’intervalle ]-π ; π] s’appelle la mesure principale.
Mesure principale d’un angle
La mesure principale d’un angle orienté est celle qui appartient à l’intervalle ]-π ; π].
Dans l’article précédent sur le cercle trigonométrique, nous avions vu comment placer les principaux angles :
Ces angles sont très importants : ce sont ceux dont il faut connaître par cœur la valeur du cosinus et du sinus. Ils appartiennent tous à l’intervalle ]-π ; π].
La question à laquelle nous souhaitons répondre est la suivante : si on nous donne une mesure d’angle supérieure à π ou inférieure à -π, comment fait-on pour trouver sa mesure principale ?
Plusieurs méthodes existent, voici la plus rapide et efficace que j’ai rencontrée en lisant les cours des professeurs de mes élèves. Je vais l’expliquer avec quelques exemples.
Exemple 1
Trouver la mesure principale de .
- A l’aide de la calculatrice, on effectue :
77÷3 = 25,666… - On cherche le nombre pair le plus proche de ce résultat, c’est à dire 26.
étant supérieur à π, on va donc retrancher 26π.
- On effectue le calcul :
- La mesure principale de
est donc
.
On pourra finalement écrire : .
Exemple 2
Trouver la mesure principale de .
- On effectue : 95÷6 = 15,833…
- On cherche le nombre pair le plus proche de ce résultat, c’est à dire 16.
étant inférieur à -π, on va donc ajouter 16π
- On effectue le calcul :
- La mesure principale de
est donc
.
On pourra écrire : .
Module 2π & mesure principale : l’explication en vidéo
Tout est-il bien clair ? N’hésitez-pas à poser vos questions en commentaire !
Fondateur et professeur aux Cours Thierry, j’enseigne les mathématiques depuis 2002. D’abord comme professeur particulier, à présent j’anime une équipe de professeurs au sein des Cours Thierry afin de proposer un accompagnement scolaire en mathématiques, physique-chimie et français.


Pour la mesure principale pourquoi l’intervalle est ouvert en -pi ?
Pour le même point, on avait le choix entre -π ou π, et on préfère π, voilà pourquoi !