Définition du nombre dérivé
Bien que la notion de « limite » ne soit plus définie dans le programme de 1ère , le nombre dérivé d’une fonction f en a, noté f'(a) est le résultat du calcul d’une limite :
Avant de poursuivre, nous allons d’abord digérer cette formule très abstraite avec une vidéo donnant l’interprétation graphique de ce calcul !
Interprétation graphique du nombre dérivé
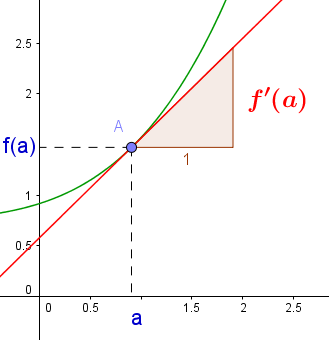
Comme expliqué dans la vidéo, le nombre dérivé de f en a, noté f'(a) est le coefficient directeur à la tangente à Cf au point d’abscisse a. (Cf désignant la courbe représentative de la fonction f).
Sur l’image ci-dessous, la courbe Cf est tracée en vert, la tangente au point d’abscisse a en rouge, son coefficient directeur est donc f'(a) :
Exemple simple du calcul d’un nombre dérivé
Prenons la fonction f définie par f(x)=x²
Voici les quelque lignes de calcul permettant d’obtenir le nombre dérivé de f en a :
Gloups !
Devra-t-on à chaque fois qu’on a affaire à la fonction carré refaire ce calcul ?
Du nombre dérivé à la fonction dérivée
Non on ne refera le même calcul à chaque fois ! On retiendra par cœur que pour la fonction carré, f'(a)=2a ou encore que lorsque f(x)=x² alors f'(x)=2x.
Ce processus automatique qui permet d’associer un nombre x à un nombre dérivé f'(x) s’appelle la fonction dérivée.
Ainsi la fonction dérivée de la fonction carré est 2x. Et la fonction dérivée d’une fonction affine du type mx+p est m, etc. Ci-dessous une liste non exhaustive des fonctions dérivées, au programme de 1ère.
x est la variable.
m, p et k sont des constantes réelles.
n est un nombre entier non nul.
u et v sont des fonctions.
Fondateur et professeur aux Cours Thierry, j’enseigne les mathématiques depuis 2002. D’abord comme professeur particulier, à présent j’anime une équipe de professeurs au sein des Cours Thierry afin de proposer un accompagnement scolaire en mathématiques, physique-chimie et français.
Post Scriptum : vous pouvez essayer d’utiliser vous-même le fichier geogebra de la fonction utilisée dans la vidéo, cliquez sur le lien suivant :
https://ggbm.at/bgH7VEKZ