Pour un acteur du soutien scolaire, le théorème des valeurs intermédiaires est du pain béni : bien qu’il laisse souvent perplexe les élèves, il est facile à expliquer, facile à appliquer, a peu de variantes ou de pièges et il est très souvent attendu au bac : le TVI ou comment récolter facilement des points en terminale !
Explications et énoncés du TVI et de son corollaire
Le théorème des valeurs intermédiaires
L’explication de ce théorème est tellement évidente avec un schéma !
J’ai tracé ci-dessous en bleu la courbe représentative d’une fonction f continue sur un intervalle [a;b]. (« Continue » signifie qu’elle a pu être tracée sans lever le crayon, ce qui est le cas de presque toutes les fonctions étudiées au lycée). J’ai placé un nombre k entre f(a) et f(b).
Si vous pensez qu’il est évident que dans ces conditions nous allons pouvoir trouver des antécédents à k (notés c1, c2 et c3 sur le graphique) c’est que vous avez déjà compris le théorème !
Les hypothèses du théorème sont :
- f est continue sur [a;b]
- k est compris entre f(a) et f(b).
Et la conclusion : k admet au moins un antécédent.
Formulation alternative de la conclusion : l’équation f(x)=k admet au moins une solution.
Bon c’est bien mais on n’utilise pour ainsi dire jamais ce théorème en exercice… Nous allons donc nous concentrer sur son corollaire !
Le corollaire du TVI
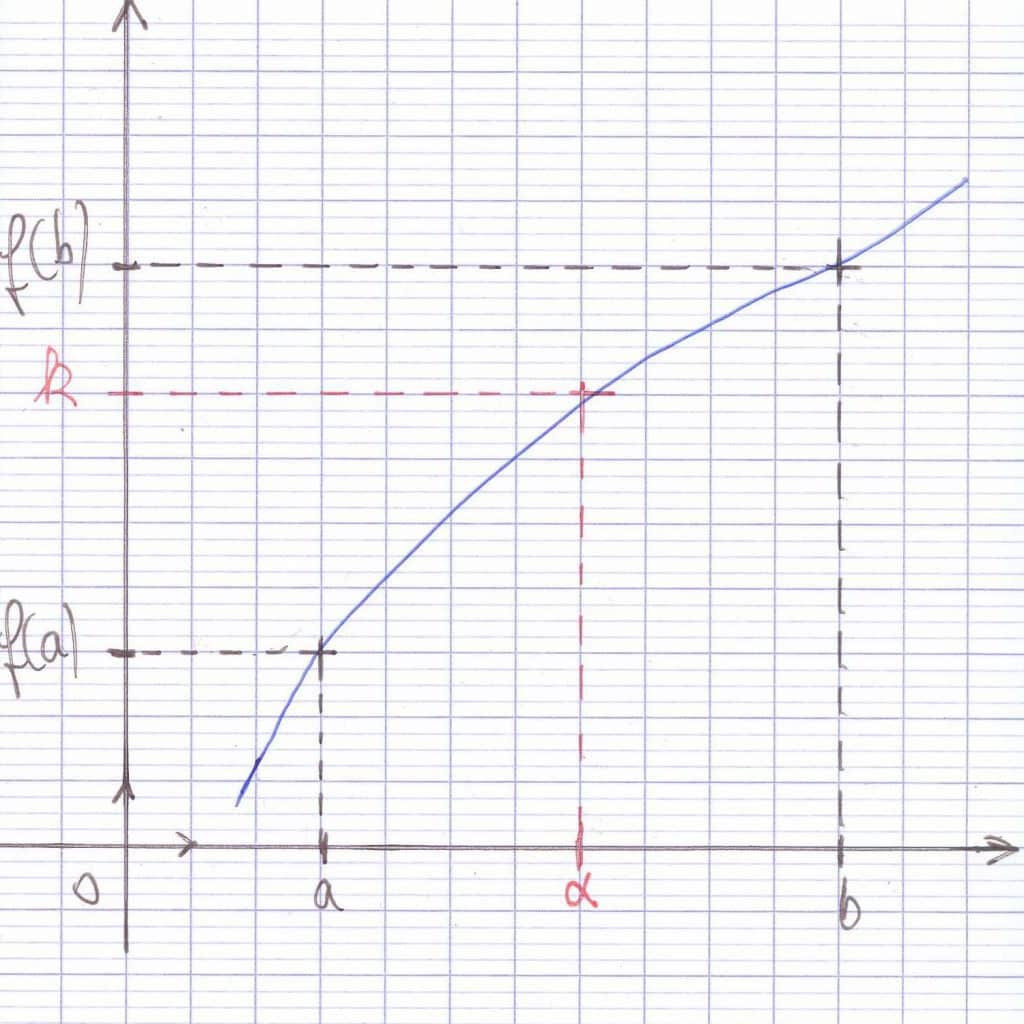
Nous savons donc que f est continue sur [a;b] et que k est compris entre f(a) et f(b). Nous ajoutons une condition supplémentaire : f est strictement croissante sur [a;b] comme le montre le graphique ci-dessous.
Et dans ce cas, comme on peut le voir sur le graphique, k admet un antécédent unique α.
NB : f pourrait aussi être strictement décroissante.
Application du corollaire aux exercices
Comment savoir quand il faut utiliser ce théorème ?
La question qui fait appel au TVI est presque toujours formulée de la même façon : montrer que l’équation f(x)=k admet une unique solution sur [a;b]. Et dans la plupart des cas il s’agit de l’équation f(x)=0. Par exemple :
Montrer que l’équation f(x)=0 admet une unique solution α sur [0;+∞[.
Comment faut-il rédiger ?
Exemple 1 : antécédent d’un nombre k pour une fonction croissante
Nous nous plaçons dans le cas d’une fonction croissante.
Montrer que l’équation f(x)=k admet une unique solution sur [a;b].
Bien penser à la formulation de trois hypothèses :
- f est continue sur [a;b]
- f est strictement croissante sur [a;b]
- Je calcule f(a)=…. et f(b)=…. et je remarque donc que k ∈ [ f(a) ; f(b) ].
Donc, d’après le théorème des valeurs intermédiaires, l’équation f(x)=k admet une unique solution sur [a;b].
Exemple 2 : antécédent de 0 pour une fonction décroissante
Nous prenons cette fois le cas d’une fonction décroissante, avec f(0)=1 et :
Montrer que l’équation f(x)=0 admet une unique solution α sur [0;+∞[.
On rédige pareillement :
- f est continue sur [0;+∞[
- f est strictement décroissante sur [0;+∞[
- Je calcule f(0)=1 et
et je remarque donc que 0∈]-∞;1].
Donc, d’après le théorème des valeurs intermédiaires, l’équation f(x)=0 admet une unique solution sur [0;+∞[.
A quoi cela va-t-il servir dans la suite de l’exercice ?
Le théorème des valeurs intermédiaires nous a permis d’affirmer que f(x) prend la valeur 0 : cela correspond à un changement de signe de f(x). Alors l’analyse du tableau des variations de f, couplée à la recherche des zéros, nous donne le signe de f(x).
C’est ce que j’explique dans la dernière partie de la vidéo ci-dessus (à 11:41).
N’hésitez pas à poser vos questions en commentaires !