Les premières notions de trigonométrie surviennent au collège en classe de 3ème où sont présentés les nouveaux opérateurs que sont le cosinus, le sinus et la tangente dans un triangle rectangle. Le cercle trigonométrique lui-même n’apparaît qu’en classe de seconde, puis est approfondi en 1ère. En terminale les élèves sont censés bien le connaître, pour l’utiliser dans l’étude de fonctions trigonométriques ou pour les arguments des nombres complexes, mais bien souvent ce n’est pas le cas.

Prenons donc une heure de temps pour revoir l’essentiel sur le cercle trigonométrique : il est important et pas si difficile de se sentir à l’aise sur le sujet !

Qu’est-ce-que le cercle trigonométrique ?

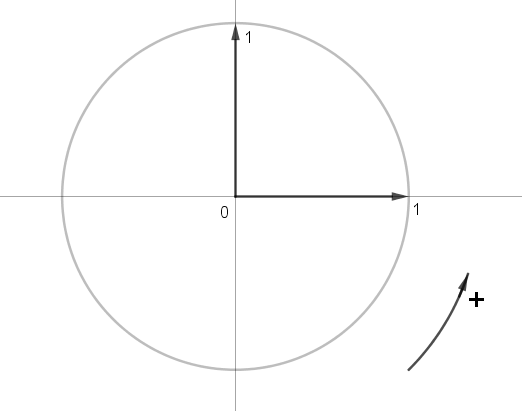
Le cercle trigonométrique est un cercle de rayon 1 dont le centre est aussi l’origine d’un repère orthonormé. Ce cercle est orienté : le sens positif ou sens direct est le sens contraire des aiguilles d’une montre.

Ci-dessous le cercle orienté et son repère orthonormé :

Des angles orientés en radians

A présent visualisons des angles qui ont pour sommet le centre du cercle (ou l’origine du repère) et dont un des côtés est confondu avec l’axe des abscisses. Par exemple ci-dessous est représenté en rouge un de ces angles dont la valeur est x :

Comme l’indique la flèche, ces angles sont orientés , c’est à dire qu’ils peuvent donc être positifs ou négatifs : positifs lorsqu’en partant toujours de l’axe des abscisses l’angle tourne dans le sens direct , négatifs quand il sont dirigés dans le sens indirect.

Comme le cercle a pour rayon 1, son périmètre vaut 2π. Un angle en radians correspond à la longueur de l’arc de cercle sur le cercle trigonométrique. Ainsi l’angle qui fait le tour complet (360°) vaut 2π radians. Un demi-tour de cercle vaut π radians et un quart de tour vaut π/2 radians.

Les quarts de tours sont coupés en 2 angles égaux pour obtenir les mesures π/4 et 3π/4, puis en 3 angles égaux pour obtenir les mesures π/6, π/3, 2π/3 et 5π/6.

Avec ces angles remarquables, nous obtenons  le cercle trigonométrique ainsi gradué :

Il est important de connaître par cœur la position de ces angles remarquables sur le cercle trigonométrique.

Cosinus et sinus d’un angle

Un angle x en radians permet dont de placer un point M sur le cercle trigonométrique. Dans le repère orthonormé, ce point M a une abscisse et une ordonnée qui sont respectivement le cosinus de l’angle x (cos x) et son sinus (sin x).

Après avoir appris la position des angles remarquables, il faut aussi apprendre les valeurs des cosinus et des sinus de ces angles. Les valeurs à retenir sont , , ,  et .

5 valeurs seulement car plusieurs angles ont les même valeurs de cosinus ou de sinus. Je les donne à lire directement sur le cercle trigonométrique : c’est ainsi la meilleure façon de les retenir, en se représentant le cercle dans la tête ou en le redessinant sur un brouillon.

Les lignes vertes indiquent les angles qui ont le même cosinus ou sinus. Attention à ne pas confondre les valeurs des angles avec celles des cosinus et sinus.

Il arrive parfois que je demande aux élèves d’apprendre certaines formules sans se poser de questions car le plus important est de simplement les appliquer. Mais dans le cas présent, la construction du cercle et sa compréhension sont nécessaires à son apprentissage. Je vous invite donc à regarder la vidéo réexpliquant sa construction afin de vous aider à l’apprendre.

Contactez-nous pour plus d'informations

Thierry

Fondateur, professeur de mathématiques aux Cours Thierry

Fondateur des Cours Thierry, j'enseigne les mathématiques depuis 2002. D'abord comme professeur particulier, à présent j'anime une équipe de professeurs au sein des Cours Thierry afin de proposer un accompagnement scolaire en mathématiques, physique-chimie et français.